On this page I want to document all of the things logicians and philosophers use to find the truths and falsities of their arguments. Here it starts. More examples, illustrations and explanations on sentential and predicate logic coming soon.
Symbols of Logic I am going to show the truth table to each connection because to do truth tables, you have to know how each connection gives truth and false values between letter variables.
1) ~ this squiggly symbol means the negation of something. So if P is true what is ~P? False. Here is the truth table for propositions just containing the ~ symbol.
P ~ P
T F T
F T F
Looking at this truth table, the ~ symbol just reverses the truth of falsity of the object/thought discussed. I call this ~F Logic page ~F because this reads “the negation of falsity”. In philosophy and logic, we want to negate falsities to get to the truth right? That is my reasoning for calling this logicians guide ~F.
2) If…then Symbol(s)- –> or ⊃
The arrow or the sideways u signifies that if theres something, the next thing concludes. If this then that. Whenever you are doing a truth table, fill in all the T’s and F’s of the letter variables themselves, then decide what the connection symbol truth is. Heres the truth table for the if/then.
P ⊃ Q
T T T
T F F
F T T
F T F
The only time the inference is false in a if/then proposition is when the first variable is true and then the second is false.
*Side note*
Heres a truth table of the first two symbols explained here, combined. Read: If P then not Q.
P ⊃ ~ Q
T F F T
T T T F
F T F T
F T T F
And also, sometimes people use 1 and 0 for T and F. I dislike that method. It confuses me.
3) Or – v (for either one) v (for one of the two)
v is hard to do a truth table for because it requires that only one of the two things be true. v is easy to do truth tables for because if there is two variables and one is true, the inference will be a true statement. The only time the or connection will yield falsity is when both variables are false. Truth table:
P v Q
T T T
T T F
F T T
F F F
Think about this in terms of the algebraic connection of Union. This is just like that but this is logic.
4) And- . or &
Think about this in terms of the algebraic connection of Intersection. This is also like that. Truth table:
P . Q
T T T
T F F
F F T
F F F
The and and or logic connections are similar because, if its or, one truth in the bunch makes the whole proposition true, while if its and, one falsity in the bunch makes the whole proposition false.
Heres a truth table of everything so far:
P v ~Q ⊃ ~P . Y
T T F T F F T F T
T T T F F F T F T
F F F T T T F T T
T T F T F F T F F
F T T F T T F T T
F F F T T T F F F
T T T F F F T F F
F T T F F T F F F
5) If/Then both ways – ↔
If you have P –> Q you know what is if and what is the then.↔ indicates that this if then relationship can be used both ways so P↔Q signifies: P –>Q and/or Q –>P. Truth table:
P ↔ Q
T T T
T F F
F F T
F T F
6) Therefore- ⊢
This symbol of a turnstile signifies that theres this, therefore, theres this too. The turnstile does not have a truth value, and cannot be represented for its truth or falsity in a truth table. It just says this therefore this.
these are often put back to back the vertical parts facing each other to represent two turnstiles. This back to back turnstile represents that P therefore Q and/or Q therefore P. I dont use this symbol much in logic.
On the ~F Logic page, I will do a lot more examples of truth tables like the big one above.
Predicate based Logic
This form of logic involves expressions where the existence of objects and their tendencies are shown.
Two kinds of quantifiers begin each expression
A universal quantifier is shown by the symbol ∀ and a variable is next to it, then the expression follows. This upside down A signifies the word ‘every’.
An existential quantifier is shown by the symbol ∃ and a variable next to it, then the expression follows. This backwards E signifies the word ‘some’. ∃! signifies that exactly one thing in existence qualifies in this expression.
Heres some examples of this predicate based logic:
∀xPx read all things are P
∀x(Px –>Qx) read All P’s are Q’s/ Every P is a Q/ If its a P, its a Q/ Only P’s are Q’s/ Any P is a Q/ Everything that is P is Q
∀xAx(Dx . Cx) All A’s are D’s and C’s
∀xAx(Dx v Cx) All A’s are either D’s or C’s
∃xAx Some things are A/ Something is an A
∃x(Bx . Cx) Some B’s are C’s
∃x(Bx –>Cx) Some B’s are C’s
x is put by the existential quantifier and the upper case descriptive variables because x signifies the actual object in discussion.
∃x(Bx v Cx) Some things are B’s or C’s
∃!x(Bx –>Cx) Exactly 1 B is a C
∃!xFx Exactly one thing is an F
Predicate based logic is best learned by learning to take English and turning it into a predicate based logic expression and taking the expressions and making scenarios to fit them.
Heres a few from English to predicate logic:
1) All people are good or bad
2) All things are created.
3) All whales are not fish.
4) Some people are schizophrenic
5) Most people are men or women
6) Exactly one reptile has white scales and a blue tongue
7) If some things are good, then some things are bad
![]() Some things are finite, therefore at least one thing is infinite
Some things are finite, therefore at least one thing is infinite
9) If all things come into existence, then all will come out of existence.
10) All birds are blue, therefore a jaybird is blue.
Do n0t scroll down anymore if you want to figure out the above 10 questions. All of the answers are below this sentence.
Answers: random variables are assigned to random things
1) ∀xPx(Gx v Bx)
2) ∀x(Ex –> Cx)
3) ∀x( Wx –> ~Fx)
4) ∃x( Px –> Sx)
5) ∃xPx( Mx v Wx)
6) ∃!xRx( Wx . Bx)
7) ∃x( Gx ⊃ Bx)
![]() ∃x( Fx ⊢ Ix)
∃x( Fx ⊢ Ix)
9) ∀x( Ix ⊃ Ox)
10) ∀xBx(Blx ⊢ Jbx)
I think In logic that you should be able to put lowercase letters next to your uppercase variables so thats what I did for #10. B signifies birds, Bl signifies blue and Jb signifies jaybirds and blue. The variable B was already used so I picked variables with extra letters. Is that okay to do ? I think so.
Lets do that process vice versa
I will give a predicate logic expression and you figure out some scenarios that fit the expression.
1) ∀xMx( (Px v Qx)⊃ ~Zx)
2) ∃!x(Px –> Yx)
3)∃xAx( (Bx . Qx) ⊃ ~( Bx . Px))
Okay so 1 and 3 might be a little difficult but 2 is easy. Heres my scenarios for these logical expressions:
1) If all men (Mx) are either stupid (Px) or shallow (Qx), then all men are not compassionate ( ~Zx ).
2) Exactly one North American colubrid snake (Px) is venomous (Yx).
3) In some shoes (Ax), if a shoe is sporty (Bx) and girlie (Qx), then the shoe cannot be sporty (Bx) and high heeled (Px)
More examples of truth tables, sentential logic, predicate logic, and going from English to logic expressions coming to the ~F Logic page on this site.
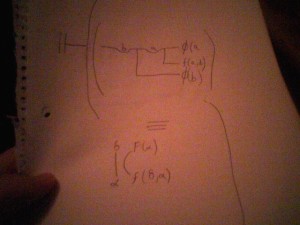
Gottlob Frege was a big influence in logic and mathematics especially when he came up with this conceptual notation for logic and its propositions. There is not really a way to type out this conceptual notation, and doing it in a Paint document looks terrible, so the best I can do in showing this conceptual notation is to write it on paper and take photos of it and upload them (regardless of how low quality of the photos are). Hopefully, the pics of the conceptual notation are enough to explain Frege’s notation.
I wanted to get my thumb out of there while doing this. I wish I could type it or do it somehow on the computer so that these low quality photos of pieces of paper would not be necessary, but for now and these purposes, it suffices.
Look at the middle figure, the one with the line and the A. This is the simplest of Frege’s conceptual notation. It identifies the essence of ideas and existences of A. No real judgment is made, so no certain proposition is declared. Now look at the top one, the lines with the A, B and C. This denotes an actual judgment so an actual proposition is made. A is the main thing discussed. The top figure translates to: If A exists, then a B exists. If B exists, then a C exists. The vertical bar at the beginning of the figure denotes that a judgment or certainty is made, unlike the line with the A where only vague essences are stated to exist. Considering the middle figure, most of Frege’s notation looks like this. Something will branch off of the top component or existence. It often becomes extensive and complicated where it is often split into two parts and worked out to find an actual meaning. I will post some of those complicated extensive notation examples in the future, but for now my aim is to show Frege’s conceptual notation and the things it can cooperate about each existence.
Look at the bottom figure. It looks kind of like the top figure. It denotes that if A, then B, except for the vertical bar in the area after A branches off to B. This lonely vertical bar denotes negation. So this translates: If not A, then B. Just because the negation bar is on the A side, it does not mean that the negation for sure sits with A. It could translate: If A, then not B. If the negation bar was before the branch of A to B, it would definitely negate A without possibility of negation of B. If there was a negation bar on each side of the B branch, A ‘s negation would cancel and no negation would exist. Hopefully the figures above and my explanation give the gist of what Frege’s notation is supposed to explain in each branch and bar. This gets more complicated.
Usually, notation in Frege does not just deal with single variables denoting one existence, component or essence. A function of these existences is usually denoted by certain symbols in this type of notation. The top figure I could have just typed out. This is one example of a function. These functions in Frege’s notation usually denote relations between variables or properties of functions in variables. The top figure F(A) denotes A has a property F function. The function of the Greek letter phi and A and B denotes that A and B relate to each other by phi (Refer back to the Pics for thought page to see the relation sequence of Wittgenstein because A and B relate to each other in the same way as Wittgenstein shows it with existential quantifiers). The bottom figure shows a judgment of phi’s property in B as a function. Notice one difference in this notation than the other ones explained in the first photo. This notation has a concave part in the middle with lowercase b in the concave space. This can also be expressed by italicizing the B in the phi(B) function judgment, but I like the concave line better with the lowercase letter. This represents a generality. The third figure above reads: For some b, phi is a property of B as a function. I like to think of this generality as an existential quantifier in predicate based logic because it denotes the word “some”. Without this concavity or italics, the universal quantifier could be used with the judgment.
The above is one figure, one judgment, one relationship. It is quite a big relationship, but you can see in the middle a 3 lined symbol in the middle. This denotes that both expressions above and below are equal to each other. The beginning of the notation here is 2 vertical bars, where normally only one judgment bar sits, but here there are 2 because 2 expressions are noted. The 2 expressions noted here: first is the regular notation I have discussed here, and the second notation is an abbreviated notation Frege used to shorten conceptual notations. The abbreviated versions involve Greek letters in place of English letters. The English letters are used in the actual notation and one is supposed to make the transition when reading the abbreviated notation and translating it to conceptual notation. Lets analyze the regular conceptual notation first. The first note is if some a, then a phi property of a exists as a function. If the previous exists, a and b relate to each other by the f function. Also, if some a, and a property phi exists in a, then some b exists in a phi property of b as a function (note how f(a,b) does not relate to phi function of b). This notation is quite a simple judgment. Frege uses the second expression to abbreviate the long conceptual notation. Here Frege uses the delta sign (δ) to show b, and the alpha letter (α) to show a. The delta and alpha are first shown in the abbreviated notation by a long vertical bar going from the delta to the alpha (different variables used intermittently). A big long ‘(‘ parentheses is used next to the long delta alpha bar to show 2 extreme functions explained by the conceptual notation. Here, F(alpha) and f(alpha,delta) is shown to note that A and B and A/B together are shown in functions as judged in the notation. Generalities are shown in any function of a and b unless it is known that they are universal. Later in the future, I will show a few conceptual notations and the abbreviated forms and set them up for practice to be converted from one form to another and I’ll give the answers. This abbreviated notation is a smaller form of the abbreviated kind.
Again, this is a doubly judged equation, where one expression equals another. This is the same thing as the first equation of notation, but the abbreviated expression is different. First lets analyze the conceptual notation. For some F, there is properties of F in y as a function and if this is true then, for some a, F exists as a property in a, and if this is true, then x and a relate to each other by f as a function. Also, for some F, you see that abbreviated notation set by itself and it has the same properties and connections as the first kind of notation like this explained. We would then have to translate this into another conceptual notation and this would be a huge conceptual notation to analyze. The abbreviated expression here shows a lambda and a beta letter one on top of the other separate by a negation ~ sign followed by the function f and x sub lambda and y sub beta. The lambda and beta separated by ~ means that y follows x. The fact that y follows x is shown by lambda and beta separated by ~ and how x has a subscript of lambda and y has a subscript of beta. The use of lambda and beta at the start of the expression and as subscripts of x and y just show that y follows x in function f. By y following x, Frege means that the conceptual notation starts at the top with functions of y. I also want to post problems on this ~F page where you are given the conceptual notation and are supposed to convert it to abbreviated notations and vice versa.
Delta and epsilon are separated by an I followed by the function of delta and epsilon. This translates to the function of delta’s relation to epsilon is the many one. The many-one means that each variable comes with a generality (a,b,e) . This many-one also denotes that the epsilon variable and the main variable a are equal to each other. Lets analyze the conceptual notation expression: for some a, b, and e, a is equal to e. and if this is true, b and a relate to each other by terms of f as a function. For some e and b, b and e relate to each other by f as a function. The many-one creates another variable besides the one presented in the abbreviated notation. This is just another kind of the small abbreviated notation like the one first discussed. There is one more abbreviation of conceptual notation to discuss.
Look at the gamma and beta organization in the abbreviated expression. There is one thing added besides the ~. A horizontal bar is added above the ~ which makes this abbreviation of notation different. This modified following notation denotes that y belongs to f starting with x. This causes an equality to be needed before the notations are presented. Generally, this would start with a y being equal to x and then it would conclude with a conditional statement with negation of that same abbreviated following notation but without the horizontal bar above the ~ putting things back to normal and leaving that following notation to be translated.
This is not for anything interesting to be argued about, but I think it is necessary to learn about to understand some later philosophers explanations.






Leave a comment